Unraveling Tennis Ball Bounce Heights with Histograms: A Data Science Exploration
Using tennis balls and histograms for a statistics exercise can be a fun and engaging way to understand and visualize data. Here’s a step-by-step guide to conducting a simple statistics exercise using tennis balls and histograms:
Objective: To analyze the bounce heights of tennis balls and create a histogram to visualize the data distribution.
Materials Needed:
- Tennis balls
- Measuring tape or ruler
- Flat surface to drop the balls from (e.g., a table or wall)
- Pen and paper or a spreadsheet for recording data
- Graphing paper or graphing software to create the histogram
Steps:
- Data Collection:
- Start by selecting a few tennis balls. It’s better to have a diverse set to capture variations in bounce heights.
- Find a suitable location with a flat surface where you can consistently drop the balls from the same height.
- Using the measuring tape or ruler, measure the height from which you will drop the balls. This will be your “drop height.”
- Drop each tennis ball from the designated drop height one at a time and observe the height of their bounce. Measure the height of each bounce using the measuring tape or ruler.
- Record the bounce height for each tennis ball. Repeat this process several times for each ball to get multiple data points.
- Data Analysis:
- Calculate the average bounce height for each tennis ball by summing up all the bounce heights and dividing by the number of data points.
- Calculate the range, which is the difference between the maximum and minimum bounce heights for each ball. This gives an idea of how much the bounce heights vary for each ball.
- You can also calculate the standard deviation to understand the dispersion of data points around the average bounce height.
- Creating the Histogram:
- Choose an appropriate range for the histogram bins. For example, if the bounce heights range from 10 cm to 50 cm, you could create bins of width 5 cm (10-14, 15-19, 20-24, and so on).
- On the x-axis of the graphing paper or software, label the bins accordingly.
- On the y-axis, label the frequency or count of tennis balls falling into each bin.
- Plot the data points on the histogram, placing each tennis ball’s bounce height into the corresponding bin.
- You can use vertical bars or rectangles to represent the frequency in each bin. The height of each bar represents the number of tennis balls in that bin.
- Interpretation:
- Analyze the histogram to understand the distribution of bounce heights. Look for patterns, such as whether the data is normally distributed, skewed, or bimodal.
- Use the histogram to identify the most common bounce height range and the range with the least frequency of occurrence.
- Conclusion:
- Summarize your findings from the data analysis and histogram. Discuss any trends or patterns observed in the bounce heights of the tennis balls.
Remember to approach this exercise with curiosity and an open mind. It’s a hands-on way to grasp the concept of histograms and gain insights into real-world data. Have fun with your statistics exercise using tennis balls and histograms!
Spreadsheet
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
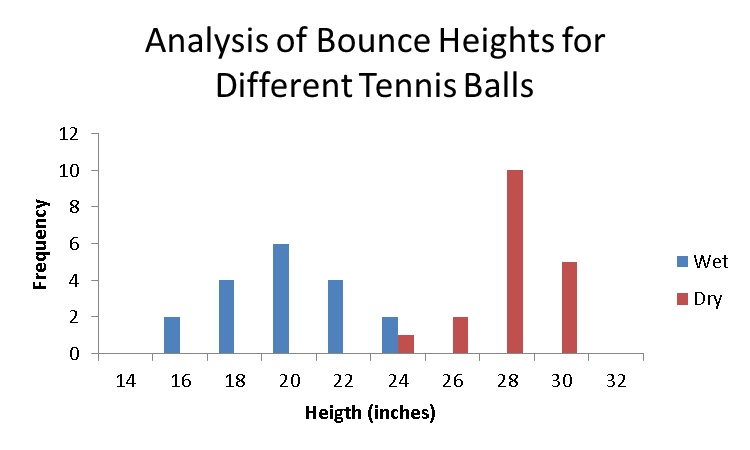
| 1 | Tennis Ball | Height Wet | Height Dry | Height | Wet | Dry |
| 2 | 1 | 14.75 | 22.50 | 12 | 0 | 0 |
| 3 | 2 | 16.00 | 24.75 | 14 | 0 | 0 |
| 4 | 3 | 17.00 | 25.25 | 16 | 2 | 0 |
| 5 | 4 | 17.25 | 26.50 | 18 | 4 | 0 |
| 6 | 5 | 17.50 | 26.75 | 20 | 6 | 0 |
| 7 | 6 | 17.60 | 26.76 | 22 | 4 | 0 |
| 8 | 7 | 18.50 | 26.80 | 24 | 2 | 1 |
| 9 | 8 | 18.80 | 26.90 | 26 | 0 | 2 |
| 10 | 9 | 19.00 | 27.50 | 28 | 0 | 10 |
| 11 | 10 | 19.25 | 27.60 | 30 | 0 | 5 |
| 12 | 11 | 19.50 | 27.60 | 32 | 0 | 0 |
| 13 | 12 | 19.50 | 28.00 | >32 | 0 | 0 |
| 14 | 13 | 20.50 | 28.25 | |||
| 15 | 14 | 20.50 | 28.30 | |||
| 16 | 15 | 21.50 | 28.50 | |||
| 17 | 16 | 21.70 | 29.00 | |||
| 18 | 17 | 22.50 | 29.20 | |||
| 19 | 18 | 23.25 | 27.00 | |||
| 20 | Min | 14.75 | 22.5 | |||
| 21 | Max | 23.25 | 29.2 | |||
| 22 | Mean | 19.1 | 27.1 | |||
| 23 | SD | 2.3 | 1.6 |
The formula =FREQUENCY(B2:B19, D2:D12) in Microsoft Excel or Google Sheets is used to calculate the frequency distribution of values in a dataset. Let’s break down the formula and understand its significance:
-
B2:B19represents the range of data values from which we want to calculate the frequency. In this case, it refers to the range of wet heights of tennis balls (B2 to B19). -
D2:D12represents the array of bins (categories) into which the data values will be counted. In this case, it refers to the range of bins or categories for the histogram (D2 to D12).
When you use this formula, it calculates how many values from the data fall into each specified bin. The output will be an array of frequencies corresponding to each bin.
For example, suppose the wet heights of tennis balls (B2 to B19) are as follows: {14.75, 16.00, 17.00, 17.25, 17.50, 17.60, 18.50, 18.80, 19.00, 19.25, 19.50, 19.50, 20.50, 20.50, 21.50, 21.70, 22.50, 23.25}.
And the bins for the histogram (D2 to D12) are as follows: {12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32}.
Using the FREQUENCY formula, it will count how many values fall into each bin:
- Bin 12-14: 0 (No values fall within this bin)
- Bin 14-16: 2 (14.75, 16.00)
- Bin 16-18: 4 (17.00, 17.25, 17.50, 17.60)
- Bin 18-20: 6 (18.50, 18.80, 19.00, 19.25, 19.50, 19.50)
- Bin 20-22: 4 (20.50, 20.50, 21.50, 21.70)
- Bin 22-24: 2 (22.50, 23.25)
- Bin 24-26: 0 (No values fall within this bin)
- Bin 26-28: 0 (No values fall within this bin)
- Bin 28-30: 0 (No values fall within this bin)
- Bin 30-32: 0 (No values fall within this bin)
- Bin >32: 0 (No values fall within this bin)
This information is crucial for creating a histogram as it represents the distribution of tennis ball wet heights across various bins. The histogram will visualize how many data points fall into each range, helping to analyze the distribution pattern and identify any trends or patterns in the data.

