Demystifying the Simplex Algorithm: Optimizing Linear Systems
Introduction: In the vast landscape of optimization techniques, the Simplex algorithm shines as a powerful tool for solving complex linear programming problems. From resource allocation to production planning and beyond, linear programming finds its application in diverse real-world scenarios where efficient decision-making is paramount. In this blog post, we embark on a journey through the realm of the Simplex algorithm, unraveling its inner workings while tackling a specific problem:
\[\begin{align*} \text{Maximize} \quad & 6x_1 + 5x_2 \\ \text{subject to} \quad & x_1 + x_2 \leq 5 \\ & 3x_1 + 2x_2 \leq 12. \end{align*}\]Unveiling Linear Programming: At its core, linear programming is a mathematical approach that seeks to optimize an objective function while adhering to a set of linear constraints. These constraints often reflect the limitations or requirements imposed by the problem’s context. Imagine a scenario where a company aims to maximize profits while considering constraints like resource availability, budget limits, or production capacities. Linear programming becomes a compass guiding decision-makers toward the most favorable outcome.
The Art of Problem Formulation: Before diving into the intricacies of the Simplex algorithm, let’s lay the foundation by converting the given problem into a standard linear programming form. This involves defining the objective function to be maximized or minimized and expressing the constraints as a system of linear inequalities. For our exploration, we’ll focus on the Objective function: \(6x_1 + 5x_2\), with the constraints \(x_1 + x_2 \leq 5 \) and \( 3x_1 + 2x_2 \leq 12\). These inequalities encapsulate the boundaries within which our solution must reside.
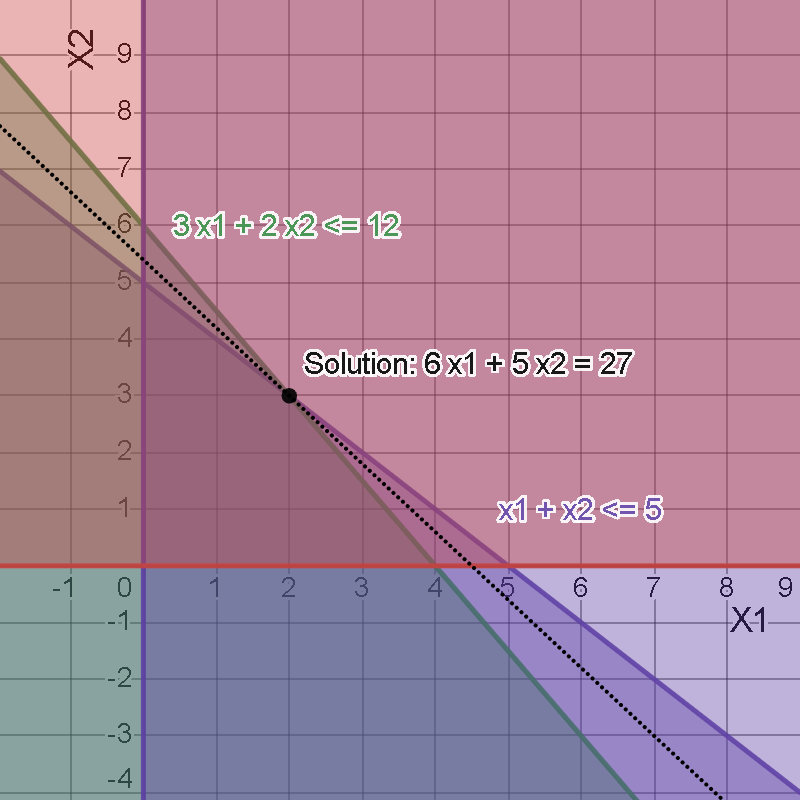
Visualizing the Feasible Region: Graphical representations offer an intuitive way to comprehend linear programming problems, especially when dealing with two variables. By plotting the constraints on a coordinate plane, we unveil a geometric region known as the feasible region. This region encapsulates all feasible combinations of \(x_1\) and \(x_2\) that satisfy the given constraints. Our task is to navigate within this region to pinpoint the optimal solution, where the objective function attains its highest value.
To graphically represent the feasible region for the constraints \(x_1 + x_2 \leq 5\) and \(3x_1 + 2x_2 \leq 12\), follow these steps:
-
Draw a coordinate plane (XY plane) with the \(x\)-axis representing \(x_1\) and the \(y\)-axis representing \(x_2\).
- Plot the line \(x_1 + x_2 = 5\):
- Find the intercept points by setting \(x_1 = 0\) and solving for \(x_2\), and vice versa.
- Plot these two points and draw the line passing through them.
- Plot the line \(3x_1 + 2x_2 = 12\):
- Similarly, find the intercept points by setting \(x_1 = 0\) and solving for \(x_2\), and vice versa.
- Plot these two points and draw the line passing through them.
- Shade the region that satisfies both constraints:
- The feasible region is the area where both inequalities are simultaneously satisfied.
- Shade the region below both lines on the graph. This shaded area represents the feasible region.
- Label the axes and any relevant points:
- Label the \(x_1\) and \(x_2\) axes appropriately.
- You can also label the intercept points and any other important points on the graph.
Please note that the feasible region is the intersection of the shaded areas under both lines. The optimal solution will lie somewhere within this region, and the Simplex algorithm will guide us to the exact optimal point where the objective function is maximized.
If you have access to graphing software or tools like Microsoft Excel or Google Sheets, you can easily create the graph by entering the equations of the lines and using their charting capabilities. Alternatively, you could use a specialized graphing tool or software designed for linear programming problems.
As we embark on our journey through the Simplex algorithm, we equip ourselves with a deeper understanding of linear programming’s core principles. In the following sections, we’ll delve into the mechanics of the algorithm, witness its iterative steps, and ultimately unveil the optimal solution that maximizes the objective function. Stay tuned as we demystify the Simplex algorithm and unlock its potential in solving real-world optimization challenges.
To build the tableau, we will follow the Simplex Method. Here’s how you can do it step by step:
| A | B | C | D | E | F | G | H | I | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | — | coeffs (cj) | 6 | 5 | 0 | 0 | — | — | — |
| 2 | coeffs | basic | x1 | x2 | x3 | x4 | rhs | theta | leave |
| Tableau 1 | |||||||||
| 3 | 0 | x3 | 1 | 1 | 1 | 0 | 5 | 5 | ☐ |
| 4 | 0 | x4 | 3 | 2 | 0 | 1 | 12 | 4 | ☑ |
| 5 | — | zj | 0 | 0 | 0 | 0 | 0 | — | — |
| 6 | — | cj-zj | 6 | 5 | 0 | 0 | — | — | — |
| 7 | — | enter | ☑ | ☐ | ☐ | ☐ | — | — | |
| Tableau 2 | |||||||||
| 9 | 0 | x3 | 0 | 1/3 | 1 | -1/3 | 1 | 3 | ☑ |
| 10 | 6 | x1 | 1 | 2/3 | 0 | 1/3 | 4 | 6 | ☐ |
| 11 | — | zj | 6 | 4 | 0 | 2 | 24 | — | — |
| 12 | — | cj-zj | 0 | 1 | 0 | -2 | — | — | — |
| 13 | — | enter | ☐ | ☑ | ☐ | ☐ | — | — | — |
| Tableau 3 | |||||||||
| 15 | 6 | x1 | 1 | 0 | -2 | 1 | 2 | — | — |
| 16 | 5 | x2 | 0 | 1 | 3 | -1 | 3 | — | — |
| 17 | — | zj | 6 | 5 | 3 | 1 | 27 | — | — |
| 18 | — | cj-zj | 0 | 0 | -3 | -1 | — | — | — |
Step 1: Write the Initial Linear Program (LP) The given linear program is:
\[\begin{align*} \text{Maximize} \quad & 6x_1 + 5x_2 \\ \text{subject to} \quad & x_1 + x_2 \leq 5 \\ & 3x_1 + 2x_2 \leq 12. \end{align*}\]Step 2: Introduce Slack Variables We will introduce slack variables to convert the inequalities into equations. Let x3 and x4 be the slack variables for the first and second constraints, respectively. Then the constraints become:
- \(x_1 + x_2 + x_3 = 5 \)
- \(3x_1 + 2x_2 + x_4 = 12 \)
Step 3: Set Up the Initial Tableau We will create the initial tableau using the coefficients of the variables in the objective function and constraints. The tableau will have the following structure:
| x1 | x2 | x3 | x4 | RHS | |
|---|---|---|---|---|---|
| x3 | 1 | 1 | 1 | 0 | 5 |
| x4 | 3 | 2 | 0 | 1 | 12 |
The values in the first row correspond to the coefficients of the objective function, and the remaining rows represent the coefficients of the constraints.
Step 4: Determine Pivot Column and Pivot Row Calculating \(z_j\) and \(c_j - z_j\) involves key steps in the Simplex algorithm, aiding in the decision-making process for variable movement within the basis. Here’s a brief overview of how to calculate these values:
Calculating \(z_j\) (Objective Function Coefficients in Basis):
- For each basic variable in the current iteration, determine its coefficient in the objective function.
- Multiply the coefficient of each basic variable by the value in its respective column of the tableau.
- Sum up the products obtained in step 2 to calculate the values of \(z_j\) for column.
Calculating \(c_j - z_j\) (Relative Cost or Reduced Cost):
- Subtract the value of \(z_j\) for each basic variable (calculated earlier) from its respective coefficient in the objective function \(c_j\).
- The result is the reduced cost \(c_j - z_j\) for each variable.
- These reduced costs help determine whether the current solution is optimal or if improvements can be made by changing the basic variables.
In summary, \(z_j\) represents the contribution of each basic variable to the objective function, while \(c_j - z_j\) indicates how much the objective function coefficient of each variable can be improved. Calculating these values assists in identifying which variable should enter or leave the basis during the pivot operations, ultimately guiding the algorithm toward an optimal solution. Calculate the ratios of the right-hand side (RHS) values to the coefficients of the pivot column.
The pivot column is the one with the greatest \(c_j-z_j\). In this case, the greatest values is 6 in the first column, so we’ll use that as the pivot column.
Theta Ratios:
- Row x3: 5 / 1 = 5
- Row x4: 12 / 3 = 4
The smallest ratio is 4, so we choose the second row (corresponding to constraint 2) as the pivot row.
Step 5: Perform the Pivot Operation To perform the pivot operation, divide the pivot row by the pivot element (3 in this case) to make the pivot element equal to 1. Then use row operations to make all other elements in the pivot column equal to zero.
New Tableau:
| x1 | x2 | x3 | x4 | RHS | |
|---|---|---|---|---|---|
| x3 | 0 | 1/3 | 1 | -1/3 | 1 |
| x1 | 1 | 2/3 | 0 | 1/3 | 4 |
Step 6: Calculate Ratios and Determine New Pivot Column Calculate the ratios again for the new tableau. The greatest coefficient in the \(cj-zj\) row is now 1 in the second column (x2). Calculate the ratios:
Theta Ratios:
- Row x3: 1 / 1/3 = 3
- Row x1: 4 / (2/3) = 6
The smallest ratio is 3, so we choose the first row as the new pivot row.
Step 7: Perform the Second Pivot Operation Perform the pivot operation again to make the pivot element equal to 1 and make all other elements in the pivot column equal to zero.
New Tableau:
| x1 | x2 | x3 | x4 | RHS | |
|---|---|---|---|---|---|
| x1 | 1 | 0 | -2 | 1 | 2 |
| x2 | 0 | 1 | 3 | -1 | 3 |
Now the tableau is in the optimal form, and the objective function is maximized. The optimal solution is x1 = 2, x2 = 3, and the maximum value of the objective function is 27.
This is the basic process to set up the initial tableau and perform the simplex method for the given linear programming problem. Further iterations may be needed to reach the optimal solution if the problem is more complex or has additional constraints.

