Exploring XOR Neural Networks with Python itertools
Introduction:
Neural networks play a crucial role in machine learning and artificial intelligence. Understanding the behavior of different neural network architectures is essential for developing robust models. In this blog post, we’ll delve into the XOR (exclusive OR) function and explore its implementation using Python, itertools, and Numpy.
Code Overview:
The provided Python code utilizes the itertools library to generate all combinations of a given set of choices (1, -1, 0). These combinations serve as weights for a neural network, which will be employed to implement the XOR function. The XOR function is constructed with a hidden layer using the rectified linear unit (ReLU) activation function and an output layer with the identity activation function.
from itertools import product
import numpy as np
# Define the set of choices (1, -1, 0)
choices = [1, -1, 0]
# Generate all combinations of the set of choices
combinations = list(product(choices, repeat=9))
# Define the ReLU activation function
def relu(x):
return np.maximum(0, x)
# Define the identity activation function
def identity(x):
return x
# XOR function implementation
def xor_function(X1, X2, w):
w1, w2, w3, w4, w5, w6, w7, w8, w9 = w
# Calculate the values of the hidden layer
X3 = relu(w1 * X1 + w3 * X2 + w7)
X4 = relu(w2 * X1 + w4 * X2 + w8)
# Calculate the value of the output layer
return identity(w5 * X3 + w6 * X4 + w9)
# Iterate over all weight combinations
for w in combinations:
results = [
xor_function(0, 0, w),
xor_function(0, 1, w),
xor_function(1, 0, w),
xor_function(1, 1, w)
]
# Check if the XOR function produces the desired output
if results == [0, 1, 1, 0]:
print("Found a valid set of weights:")
print("Weights:", w)
print("Results:", results)
Explanation:
-
The code starts by importing the necessary libraries: itertools for generating combinations and numpy for numerical operations.
-
The XOR function is implemented with a hidden layer consisting of two ReLU-activated neurons and an output layer with the identity activation function.
-
The code iterates over all combinations of weights generated by itertools and applies them to the XOR function.
-
For each set of weights, the XOR function is evaluated for all possible input combinations for X1 and X2 (0,0), (0,1), (1,0), and (1,1).
-
If the XOR function produces the expected output [0, 1, 1, 0], the set of weights and corresponding results are printed.
Conclusion:
This blog post has demonstrated the use of itertools and Numpy in generating combinations of weights for a neural network. The XOR function serves as an example of a simple neural network, highlighting the importance of appropriate weight configurations for specific tasks. Understanding and experimenting with neural network architectures are essential steps in mastering the field of machine learning and artificial intelligence.
Visualization:
import networkx as nx
import matplotlib.pyplot as plt
# Define the XOR network architecture
def xor_network_graph():
G = nx.DiGraph()
# Input layer
G.add_nodes_from(['X1', 'X2'])
# Hidden layer
G.add_nodes_from(['X3', 'X4'])
G.add_edges_from([('X1', 'X3'), ('X2', 'X3'), ('X1', 'X4'), ('X2', 'X4'), ('bias', 'X3'), ('bias', 'X4')])
# Output layer
G.add_node('Output')
G.add_edges_from([('X3', 'Output'), ('X4', 'Output'), ('bias', 'Output')])
return G
# Provided sets of weights and corresponding results
weight_sets = [
((1, -1, 1, -1, -1, -1, -1, 1, 1), [0, 1, 1, 0]),
((1, -1, -1, 1, 1, 1, 0, 0, 0), [0, 1, 1, 0]),
((-1, 1, 1, -1, 1, 1, 0, 0, 0), [0, 1, 1, 0]),
((-1, 1, -1, 1, -1, -1, 1, -1, 1), [0, 1, 1, 0])
]
# Create a subplot for each set of weights
fig, axs = plt.subplots(len(weight_sets), 1, figsize=(8, 6 * len(weight_sets)))
# Iterate over each set of weights and plot the XOR network
for i, (weights, results) in enumerate(weight_sets):
G = xor_network_graph()
pos = nx.spring_layout(G)
# Draw the network
nx.draw(G, pos, ax=axs[i], with_labels=True, node_size=700, font_size=8, font_weight='bold', node_color='skyblue', edge_color='gray')
# Highlight the edges corresponding to weights
edge_labels = {('X1', 'X3'): f'w1={weights[0]}', ('X2', 'X3'): f'w3={weights[2]}',
('X1', 'X4'): f'w2={weights[1]}', ('X2', 'X4'): f'w4={weights[3]}',
('bias', 'X3'): f'w7={weights[6]}', ('bias', 'X4'): f'w8={weights[7]}',
('X3', 'Output'): f'w5={weights[4]}', ('X4', 'Output'): f'w6={weights[5]}',
('bias', 'Output'): f'w9={weights[8]}'}
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, ax=axs[i], font_color='red')
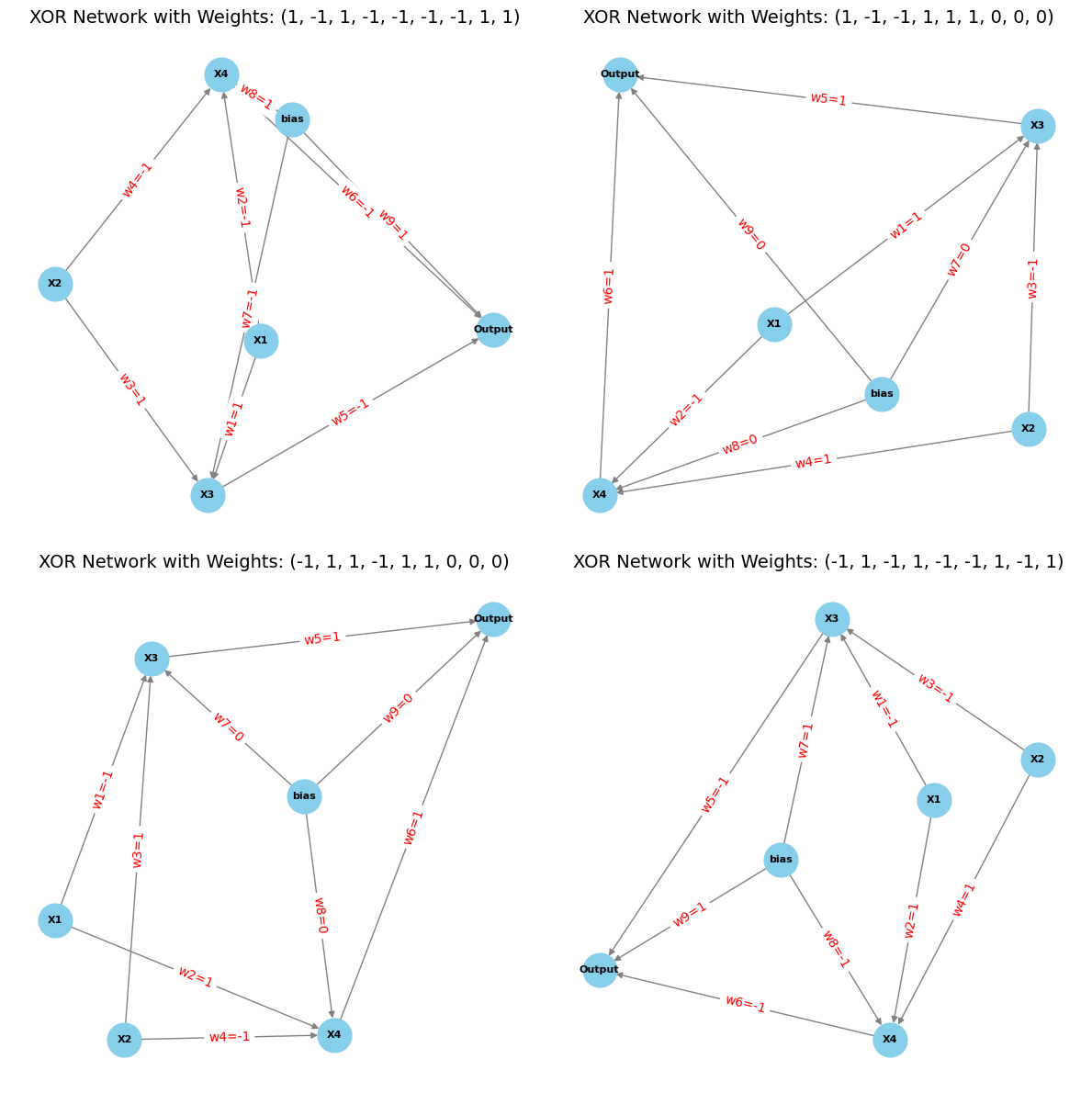
axs[i].set_title(f"XOR Network with Weights: {weights}")
plt.tight_layout()
plt.show()

