Maximizing Returns: Using Decision Trees and Expected Values for Strategic Decision Making
Introduction to Decision Analysis and Trees
In the realm of strategic decision-making, organizations often encounter complex scenarios that necessitate a structured approach for evaluation. Decision analysis, coupled with the use of decision trees, offers a systematic method to navigate through uncertainties and arrive at optimal choices.
Decision Analysis involves assessing potential outcomes, assigning probabilities to various scenarios, and quantifying the impact of decisions. It provides a structured framework for weighing alternatives and making informed choices based on both qualitative and quantitative factors.
Decision Trees serve as visual representations of decision-making processes, depicting various decision points, possible outcomes, and associated probabilities. By branching out from each decision node, decision trees illustrate the flow of decisions and chance events, facilitating a comprehensive understanding of the decision landscape. In this analysis, we utilize decision analysis techniques alongside decision trees to assess the viability of implementing a waste recycling program. Through a structured approach, we aim to provide actionable insights that drive sustainable and economically sound decisions for organizations.
The Scenario:
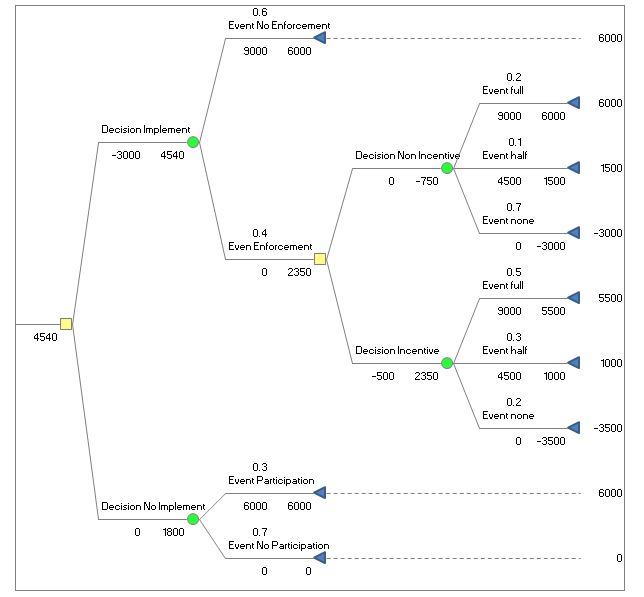
The decision whether to implement a food waste recycling program by WCo entails several outcomes. If the WCo decides against implementation, there’s a 30% likelihood that schools will autonomously participate, resulting in WCo receiving $9,000 and spending $3,000. Conversely, if WCo implements the program, there’s a 60% chance of full school participation without enforcement, yielding the same financial gains. However, there’s a 40% chance that enforcement becomes necessary. Under non-vigorous enforcement, success rates vary with a 20% chance of full success, 10% chance of half success, and 70% chance of failure, each with corresponding financial outcomes. Alternatively, under vigorous enforcement, success rates are 50% for full success, 30% for half success, and 20% for failure, with an additional cost of $500 if required, influencing the financial implications of the decision.
The decision involves several key factors:
- Implementation Decision:
- If WCo decides to implement the program, there’s a 60% chance of achieving full school participation without enforcement.
- However, there’s also a 40% chance that enforcement becomes necessary.
- Enforcement Scenarios:
- Under non-incentive enforcement, success rates vary.
- Alternatively, under incentive enforcement, success rates differ with an additional cost.
- Financial Implications:
- If WCo chooses not to implement the program, there’s a 30% likelihood that schools will autonomously participate, resulting in financial gains and expenses.
Calculating Expected Values:
To guide decision-making, let’s integrate Python code to calculate the expected values under various scenarios:
income = 9000
base_expense = 3000
incentive_expense = 500
implement_success_rate = 0.6
default_rate = 0.3
incentive_probs = [0.5, 0.3, 0.2]
incentive_factors = [1, 0.5, 0]
nonincentive_probs = [0.2, 0.1, 0.7]
nonincentive_factors = [1, 0.5, 0]
implement_success = implement_success_rate * (income - base_expense)
implement_failure_incentive = (1 - implement_success_rate) * (
incentive_probs[0] * (incentive_factors[0] * income - base_expense - incentive_expense)
+ incentive_probs[1] * (incentive_factors[1] * income - base_expense - incentive_expense)
+ incentive_probs[2] * (incentive_factors[2] * income - base_expense - incentive_expense)
)
implement_failure_non_incentive = (1 - implement_success_rate) * (
nonincentive_probs[0] * (nonincentive_factors[0] * income - base_expense)
+ nonincentive_probs[1] * (nonincentive_factors[1] * income - base_expense)
+ nonincentive_probs[2] * (nonincentive_factors[2] * income - base_expense)
)
not_implement = default_rate * (income - base_expense)
expected_values = [
implement_success + implement_failure_incentive, implement_success + implement_failure_non_incentive,
not_implement
]
max_expected_value = max(expected_values)
print("Expected Values:", expected_values)
print("Max Expected Value:", max_expected_value)
The output of this code provides the expected values associated with each scenario:
Expected Values: [4540.0, 3300.0, 1800.0]
Max Expected Value: 4540.0
Decision Analysis:
- Implementing the Program:
- Success without Enforcement (60%):
- Results in the maximum financial gains.
- Enforcement Required (40%):
- Under non-incentive enforcement:
- Success rates vary with associated financial outcomes.
- Under incentive enforcement:
- Success rates differ with an additional expense.
- Under non-incentive enforcement:
- Success without Enforcement (60%):
- Not Implementing the Program:
- Schools may autonomously participate (30%).
- Results in financial gains and expenses.
Conclusion:
Upon thorough analysis, it becomes evident that implementing the food waste recycling program yields the highest expected value. However, factors such as enforcement mechanisms and associated costs must be carefully considered. In conclusion, by weighing the financial implications, organizations like WCo can make informed decisions that align with their objectives and values.
Appendix: Tree Plan
Utilizing Tree Plan in Excel for Decision Optimization
Decision optimization often involves evaluating multiple scenarios to maximize outcomes. With the Tree Plan add-on in Excel, you can streamline this process efficiently. Here’s a quick guide on how to use Tree Plan with the provided code:
Step 1: Installing Tree Plan
- Install the Tree Plan add-on in Excel through the “Get Add-ins” or “Office Add-ins” feature.
- Follow the installation prompts to integrate Tree Plan into your Excel environment.
Step 2: Modeling the Decision Tree
- Open Excel and navigate to the Tree Plan tab.
- Define decision options and possible outcomes as nodes in the decision tree.
- Input probabilities and values associated with each node based on your scenario.
Step 3: Analyzing with Tree Plan
- Utilize Tree Plan’s analysis tools to calculate expected values and assess different decision paths.
- Explore sensitivity analyses to understand how changes in probabilities or values impact outcomes.
Step 4: Decision Making
- Evaluate the decision tree’s insights to make informed decisions based on maximizing expected values.
- Consider adjusting probabilities or values to optimize your decision strategy.
Step 5: Iterating and Refining
- Update the decision tree as new information emerges.
- Reanalyze with Tree Plan to adapt your approach and improve decision outcomes over time.
By leveraging Tree Plan in Excel, you can efficiently analyze decision scenarios like the provided code, optimizing outcomes and driving better decision-making processes.