Exploring Equidistant Points in a 2D Space using PySpark
Introduction
Equidistant points, points with equal distances to a centroid, hold significance across multiple disciplines. From aiding in geometric modeling to assisting in clustering algorithms, the identification of equidistant points unlocks a plethora of applications. In this blog post, we delve into the process of identifying these points using PySpark, a powerful distributed computing framework. Our objective is to showcase how PySpark can efficiently handle large datasets to unveil equidistant point patterns, followed by visualizations that offer insights into their spatial arrangement.
Objective of the Blog Post
This blog post aims to demonstrate how PySpark can be utilized to efficiently identify equidistant points within a two-dimensional space. By leveraging the distributed computing capabilities of PySpark, we showcase the scalability and performance of the framework in processing large datasets. Additionally, we provide visualizations of the identified equidistant points, offering readers a deeper understanding of their spatial distribution.
Identifying Equidistant Points with PySpark
Generating Random Points
To begin our exploration, let’s generate a set of random points within a specified range in a 2D space. We’ll use Python’s random module to generate these points and then write them to a file for further processing.
!pip install pyspark &> /dev/null
from pyspark import SparkContext
sc = SparkContext()
import random
# Number of random points to generate
num_points = 500
# Range for x and y coordinates
x_range = (-15, 15)
y_range = (-15, 15)
# Generate random integer points
points = [(random.randint(x_range[0], x_range[1]), random.randint(y_range[0], y_range[1])) for _ in range(num_points)]
# Write points to file
with open("data.txt", "w") as file:
for point in points:
file.write(f"{point[0]} {point[1]}\n")
This code snippet generates num_points random points within the specified range for x and y coordinates and writes them to a file named “data.txt”.
Setting up PySpark Environment
Before we proceed, let’s set up our PySpark environment by initializing a SparkContext and importing the necessary modules.
from pyspark import SparkContext
sc = SparkContext()
from pyspark.rdd import RDD
Now that our PySpark environment is set up, we’re ready to read the generated points from the file and perform operations on them using PySpark RDDs.
Processing Points with PySpark RDDs
Now that we have our random points generated and stored in a file, let’s use PySpark RDDs to process them and identify the equidistant points.
Reading Points from File
We’ll start by reading the points from the file into an RDD. Each line in the file represents a point with its x and y coordinates.
def to_tuple(point_str):
x, y = map(int, point_str.split())
return x, y
# Read points from file into an RDD
rdd = sc.textFile('data.txt')
rdd = rdd.map(to_tuple)
Here, we define a function to_tuple to convert each line of the file into a tuple of integers representing the x and y coordinates of a point. Then, we use the textFile function to read the file into an RDD and apply the map transformation to convert each line into a tuple of coordinates.
Cartesian Product
To identify equidistant points, we’ll need to compute the Cartesian product of the points RDD with itself to pair each point with every other point.
def get_cartesian(rdd):
cartesian_rdd = rdd.cartesian(rdd)
cartesian_rdd = cartesian_rdd.filter(non_duplicates)
return cartesian_rdd
def non_duplicates(pair):
return pair[0] != pair[1]
# Compute Cartesian product of points RDD
cartesian_rdd = get_cartesian(rdd)
We define a function get_cartesian to compute the Cartesian product of an RDD with itself while filtering out duplicate pairs of points. The cartesian transformation generates all possible pairs of points, and the filter transformation removes pairs where both points are the same.
Identifying Equidistant Points with PySpark
Now that we have computed the Cartesian product of the points RDD, let’s implement the logic to identify equidistant points among the pairs generated.
Calculating Distances
To identify equidistant points, we need to calculate the distance between each pair of points in the Cartesian product RDD. We’ll define a function to compute the Euclidean distance between two points.
def find_distance(pair):
(x1, y1), (x2, y2) = pair
distance = ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
return ((x1, y1), distance), (x2, y2)
# Map each pair of points to their distance
distance_rdd = cartesian_rdd.map(find_distance)
Here, we define a function find_distance to calculate the Euclidean distance between two points. We then use the map transformation to apply this function to each pair of points in the Cartesian product RDD, resulting in an RDD of tuples containing the original pair of points and their corresponding distance.
Grouping Equidistant Points
Next, we’ll group the points based on their distances to identify equidistant points. We’ll group points with the same distance into lists and filter out groups with fewer than 10 points, as they are unlikely to form meaningful patterns.
def find_equidistant(rdd):
grouped_rdd = rdd.map(lambda x: ((x[0][0], x[0][1]), (x[1],)))
grouped_rdd = grouped_rdd.reduceByKey(lambda x, y: x + y)
result_rdd = grouped_rdd.map(lambda x: ([x[0][0]]+ [v for v in x[1]] ))
result_rdd = result_rdd.map(to_sorted_points)
result_rdd = result_rdd.filter(lambda x: len(x) >= 10)
result_rdd = result_rdd.distinct()
result_rdd = result_rdd.sortBy(lambda x: x[0][0])
return result_rdd
# Find equidistant points
equidistant_rdd = find_equidistant(distance_rdd)
In the find_equidistant function, we group the points by their coordinates and distances, then filter out groups with fewer than 10 points. We also ensure that the resulting RDD contains unique equidistant point patterns and sort them for visualization.
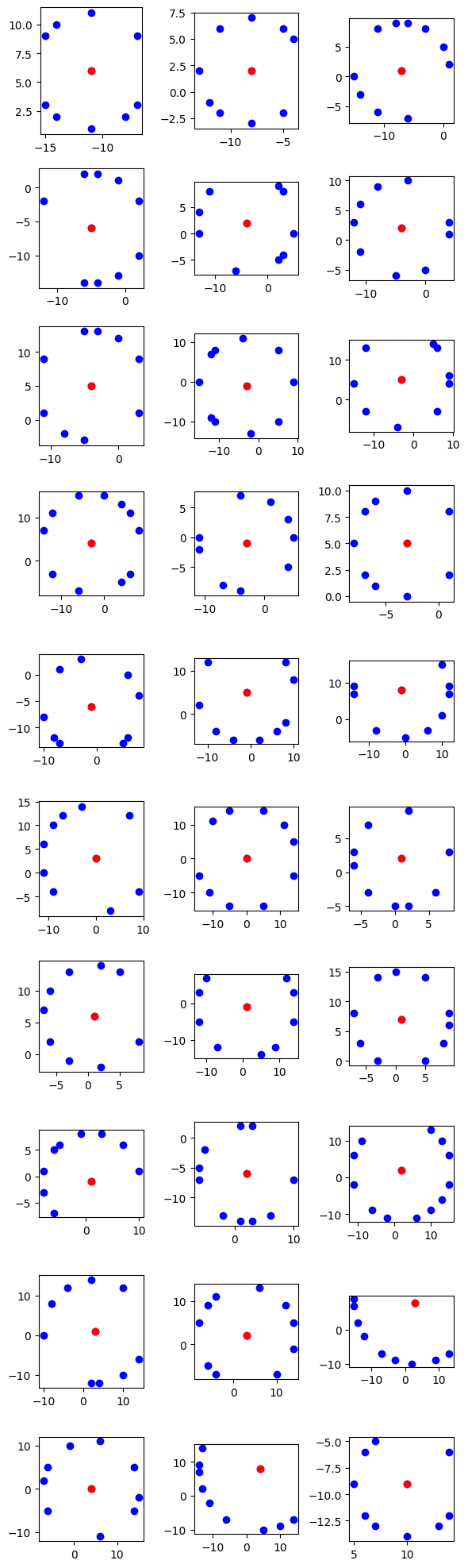
Visualizing Equidistant Points with Matplotlib
With the equidistant points identified using PySpark, let’s proceed to visualize them using Matplotlib, a popular plotting library in Python.
Plotting Equidistant Points
We’ll plot the identified equidistant points on a 2D graph to visualize their spatial distribution and patterns. Each equidistant point pattern will be represented as a separate subplot, allowing us to analyze them individually.
import matplotlib.pyplot as plt
data = equidistant_rdd.collect()
num_columns = 3 # Number of columns for subplots
num_plots = len(data)
num_rows = (num_plots + num_columns - 1) // num_columns # Calculate number of rows needed
fig, axs = plt.subplots(num_rows, num_columns, figsize=(2*num_columns, 2*num_rows))
for i, sublist in enumerate(data):
row = i // num_columns
col = i % num_columns
ax = axs[row, col]
x_values, y_values = zip(*sublist)
ax.plot(x_values, y_values, 'bo') # Plot all points in blue
ax.plot(x_values[0], y_values[0], 'ro') # First point in red
ax.set_aspect('equal') # Set same scale for x and y axes
# Hide empty subplots if the number of plots is not a multiple of num_columns
if num_plots % num_columns != 0:
for j in range(num_plots % num_columns, num_columns):
fig.delaxes(axs[-1, j])
plt.tight_layout()
plt.show()
In this code snippet, we use Matplotlib to create subplots for each equidistant point pattern. We iterate through the data collected from the equidistant RDD and plot each pattern as a set of points on a separate subplot. The first point of each pattern is highlighted in red for clarity.
Conclusion: Unveiling Patterns and Significance
In this blog post, we embarked on a journey to explore the identification of equidistant points in a 2D space using PySpark. Through a step-by-step process, we demonstrated how PySpark, a powerful distributed computing framework, can be leveraged to efficiently process large datasets.